行測數(shù)量關(guān)系：排列組合常用方法
行測數(shù)量關(guān)系：排列組合常用方法
在公務(wù)員行測考試的數(shù)量關(guān)系題目中，排列組合問題是一類很重要的題型，而其通常伴隨一些明顯的特征出現(xiàn)。今天，政華公考就通過本文為大家介紹排列組合的常用方法。
優(yōu)限法
1.應(yīng)用環(huán)境：要求元素必須在哪兒或不在哪兒，即對元素的絕對位置有要求。
2.操作方法：首先把有絕對位置要求的元素優(yōu)先進行排列組合，然后考慮其他元素的排列組合情況。
例1：一次會議某單位邀請了10名專家，該單位預(yù)定了10個房間，其中一層5間、二層5間。已知邀請專家中4人要求住二層、3人要求住一層、其余3人住任一層均可。那么要滿足他們的住房要求且每人1間，有多少種不同的安排方案？（ ）
A.75 B.450 C.7200 D.43200
【答案】D【解析】由題意，專家中有4人要求住二層、3人要求住一層，他們有絕對的位置要求，那么此題應(yīng)當(dāng)采用優(yōu)限法來解題。共有10人，4人要求住二層，
其余3人安排住剩下的3個房間，
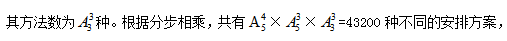故本題選D。
捆綁法
1.應(yīng)用環(huán)境：有元素要求“相鄰”。
2.操作方法：首先把要求“相鄰”的元素捆綁起來視為一個整體，與其他元素進行排列組合，然后考慮捆綁元素內(nèi)部的順序。
例2：為加強機關(guān)文化建設(shè)，某市直機關(guān)在系統(tǒng)內(nèi)舉辦演講比賽，3個部門分別派出3、2、4名選手參加比賽，要求每個部門的參賽選手比賽順序必須相連，問不同參賽順序的種數(shù)在以下哪個范圍之內(nèi)？（ ）
A.小于1000 B.1000—5000
C.5001—20000 D.大于20000
【答案】B【解析】由題意，每個部門的參賽選手比賽順序必須相連，即元素要求“相鄰”，采用捆綁法。首先把3個部門的選手分別捆綁在一起，考慮三個部門的出場順序，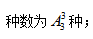
然后考慮每個部門內(nèi)部各選手的出場順序，
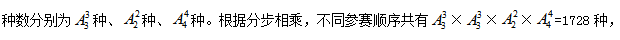計算結(jié)果顯然大于1000，小于5000。本題選B。
插空法
1.應(yīng)用環(huán)境：有元素要求“不相鄰”。
2.操作方法：先把其它可相鄰的元素進行排列組合，形成空，然后將不相鄰的元素進行插空。
例3：把12棵同樣的松樹和6棵同樣的柏樹種植在道路兩側(cè)，每側(cè)種植9棵，要求每側(cè)的柏樹數(shù)量相等且不相鄰，且道路起點和終點處兩側(cè)種植的都必須是松樹。問有多少種不同的種植方法？（ ）
A.36 B.50 C.100 D.400
【答案】C【解析】由題意，每側(cè)的柏樹要求不相鄰，采用插空法。道路每側(cè)種植9棵樹，其中6棵松樹3棵柏樹，6棵松樹形成5個空隙，將3棵柏樹插入，
本題選C。
以上就是排列組合的幾種常用方法，大家具體解題時一定要看清題干中的各種限制條件，明確哪種條件下該使用哪種方法，做到熟能生巧。
行測排列組合之異素均分問題易錯點剖析
數(shù)量關(guān)系是行測考試中難度頗高的一個板塊，其主要考察應(yīng)試者理解、把握事物間量化關(guān)系和解決數(shù)量關(guān)系問題的技能，主要涉及數(shù)字和數(shù)據(jù)關(guān)系的分析、推理、判斷運算等，其中，排列組合的異素均分問題是很多同學(xué)都很難做正確的一類題目，但只要我們研究清楚其問題的本質(zhì)，便可輕松做對此類題目。
一、從問法上識別“異素均分”問題
異素均分，就概念而言，就是把不同的元素進行平均分組。
例如：m個不同的元素，平均分為n個組，一共有多少種情況？
二、“異素均分”問題破解思路
把m個不同的元素平均分成n組，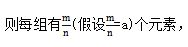
接著我們采用分步的原理來計算，首先從m個元素當(dāng)中取出a個元素，接著從剩下的元素當(dāng)中再取出a個元素，一直重復(fù)下去，每次都取a個元素，等到全部元素取完便可終止，最后再分析這個過程中所包含的情況數(shù)。
1.異素均分分堆問題
例1：某中學(xué)有8個運動員，要平均分成2組，一共有幾種分法？（ ）
A.25 B.70 C.35 D.90
【答案】C【解析】8個運動員平均分成2組，每組4人。首先從8個運動員中選出4個人，
接著從剩下的4個人中選出4個人，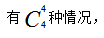
因為整個過程是分步進行的，所以總的方法數(shù)等于各個步驟的方法數(shù)相乘，
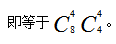但其實這樣做是存在問題的，我們可以把這8個人用abcdefgh這8個字母依次來表示，其中的一種情況可以是abcd為一組，那么剩下的efgh就自然成為另外一組了，當(dāng)然也有可能是先挑出了efgh為一組，則abcd為一組，這兩種分組方式前后對比會發(fā)現(xiàn)是同一種分組方式，都是abcd為一組，efgh為一組，所以算重復(fù)了2次，實際上的情況數(shù)為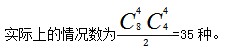
通過這個題目我們可以看出，平均分成2組，算重復(fù)了2次，如果平均分成3組，會算重復(fù)幾次呢？
例2：將紅、橙、黃、綠、藍、白6顆不同顏色的玻璃球，平均分成3堆，一共有幾種情況？（ ）
A.15 B.45 C.60 D.90
【答案】A【解析】6顆不同顏色的玻璃球等同于6個不同的元素，平均分成3堆，每堆2顆玻璃球。首先，從6顆玻璃球中取出2顆；接著從剩下的4顆玻璃球中取2顆；最后從剩下的2顆中選出2顆，同樣的我們還是選取其中的一種情況(紅橙、黃綠、藍白)來分析。
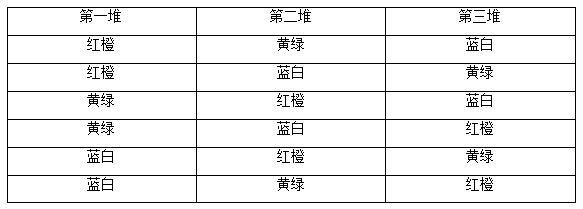
通過這個表格的簡單羅列，我們便可以清楚地發(fā)現(xiàn)這6種情況都是同一種分堆情況，即紅橙一堆，黃綠一堆，藍白一堆，算重復(fù)了6次，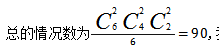
我們可以進一步總結(jié)前一個題目平均分成兩組，算重復(fù)了2次，本質(zhì)上是算重復(fù)了
本題平均分成3組，算重復(fù)了6次，
所以可以得到異素均分問題平均分成n組，
2.異素均分分配問題
例題：某公司將旗下的6名歌手兩兩組成一個隊，到三個不同的省會城市參加巡演，共有多少種不同的巡演情況？（ ）
A.15 B.45 C.60 D.90
【答案】D【解析】本題為異素均分問題，6名歌手兩個人為一個隊，即平均分成3隊。根據(jù)前面所講分成3隊，
因為3個隊是去到3個不同的城市巡演，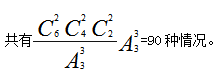
相信大家通過上述題目，能對異素均分問題有所了解，建議大家在備考期間多多練習(xí)，真正掌握這類問題，也希望能對大家的備考有所幫助。
行測排列組合不用煩，隔板模型記心間
在行測數(shù)量關(guān)系考試中，排列組合是很多人又愛又恨的一個考點，對文科生來講尤其如此，愛它是因為計算量相對不大，恨它是因為計數(shù)時經(jīng)常出現(xiàn)重復(fù)或遺漏的情況。其實排列組合中的一些問題是有固定解題思路的，也有一些常見的解題模型。本文接下來政華公考就給大家分享排列組合中一種特殊模型——“隔板模型”。
“隔板模型”的特征是：n個相同元素分給m個不同對象，每個對象至少分一個元素，求所有可能的分法。“隔板模型”的解題思路是：將n個元素排成一排，在n個元素之間形成的n-1個間隙中放置m-1塊隔板，即可把它隔成m份，這樣所有不同的插入方法就是n個相同的元素分給m個不同對象的所有情況數(shù)，為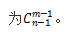
例1：共有10本完全相同的書分到4個班里，每個班至少要分到一本書，共有幾種不同分法？（ ）
A.84 B.75 C.64 D.45
【答案】A【解析】先將10本相同的書排成一排，10本書之間出現(xiàn)了10-1=9個空隙，現(xiàn)在我們用4-1=3個擋板插入這9個空隙中，就把10本書隔成4份，正好分給4個班級；從9個空選3個插入3個相同擋板，不考慮順序，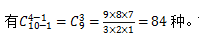
故正確答案為A。
例2：共有6本完全相同的書分到4個班里，共有多少種不同分法？（ ）
A.84 B.75 C.64 D.45
【答案】A【解析】由于會有不放書的班級，因此需要將問題轉(zhuǎn)化為標(biāo)準(zhǔn)的隔板模型。先從每個班級借一本書，則現(xiàn)在有10本書，問題就轉(zhuǎn)化為“將10本完全相同的書分給4個班，每班至少分到一本”。從10本書排成一排所形成的10-1=9個空隙里選擇3個空隙插入隔板，就把10本書隔成4份，正好分給4個班級，每個班至少一本書，則不同的分法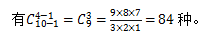
故正確答案為A。
例3：共有14本完全相同的書分到4個班里，每個班至少分到兩本書，共有多少種不同分法？（ ）
A.84 B.75 C.64 D.45
【答案】A【解析】由于每個班級至少分兩本，因此需要將問題轉(zhuǎn)化為標(biāo)準(zhǔn)的隔板模型。每個班級先發(fā)1本書，還剩10本，則問題轉(zhuǎn)化為“將10本完全相同的書分給4個班，每班至少分到一本”。從10本書排成一排所形成的10-1=9個空隙里選擇3個空隙插入隔板，就把10本書隔成4份，正好分給4個班級，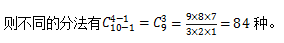
故正確答案為A。
通過上面三個例子對比，大家會發(fā)現(xiàn)雖然下面兩個例子與“隔板法”題型特征不符，但是我們可以通過轉(zhuǎn)換使其滿足條件，最終還是可以借助公式來解題。
通過對上述例題的學(xué)習(xí)，大家應(yīng)該已經(jīng)能夠感受到數(shù)學(xué)變化的神奇。希望同學(xué)們在平日的學(xué)習(xí)中能夠多多練習(xí)，真正把所學(xué)方法內(nèi)化于心，外化于行，做到信手拈來！
